Descrição do problema:
Este post é destinado a conclusão do Pipeline gráfico, que teve início no post anterior( clique aqui ), ou seja, iremos implementar todas as transformações usando coordenadas homogêneas. Foi proposto para os alunos que os mesmos implementassem um Pipeline Gráfico completo, semelhante ao usado no OpenGL, que recebesse uma malha de triângulos no espaço do objeto e os levassem para um espaço “canônico”, rasterizando a imagem formada no final, o nosso Pipeline Gráfico consiste em 6 transformações que está ilustrada abaixo:

Figura 1 - Processo de um Pipeline Gráfico
O que é Pipeline Gráfico?
Na computação gráfica 3D , o pipeline de gráficos refere-se à sequência de passos utilizados para criar uma representação raster 2D de uma cena 3D. É um dos conceitos mais importantes de computação gráfica existentes. É importante entendê-lo para dominar as APIs gráficas OpenGL e DirectX, pois diversas funções destas APIs agem sobre diferentes estágios do pipeline.
1.1- Espaço do Objeto (Object Space)
Este é o espaço aonde ocorre a modelagem do objeto a partir das primitivas geométricas. Neste espaço não há uma importância de qual sistema de coordenadas foi adotado e o objeto ainda está modelado em espaços infinitos.
1.2- Espaço do Universo (World Space)
Este espaço engloba todo universos e permite-nos expressar as coordenadas de forma absoluta, transição do sistema de coordenadas do objeto para o sistema de coordenadas 3D(mundo virtual). A sua origem é a posição da câmera.
1.3- Espaço da Câmera (Camera Space)
No espaço da câmera iremos escolher o posicionamento da câmera, o alcance de visualização e qual será tipo de projeção. Nem sempre a câmera será igual as coordenadas e assim precisaremos, transportar a cena para o plano da câmera.
1.4 Espaço de Recorte (Clipping Space)
Nesse espaço está interligada processamentos gráficos, porquê é neste espaço aonde é feito o recorte das primitivas gráfica, e com isso interferindo no processos que são feitos durante a geração desse espaço. Desde o primeiro momento, aonde começamos do espaço do objeto até ao espaço do universo, é feita diversas transformações de primitivas. Logo após é feito o posicionamento da câmera, que indicá o que será virtualizado e que posteriormente serão exibido na tela. Todas as primitivas não virtualizadas, ou seja não alcançada pela câmera serão descartadas e com isso influenciando na velocidade do processo gráfico, sem isso não seria possível a geração de cenários dos games, simuladores e animações complexas. Avalie como seria renderizar a cada frame todo o cenário de GTA 5 ou de Watch Dogs, haja hardware para aguentar.
1.5- Espaço Canônico (Canonical Space)
O espaço canônico é o espaço que basicamente faz o
mapeamento dos pontos para centralizar o volume gerado na etapa anterior para o espaço canônico, formando o Volume Canônico. Já fizemos muitos movimentos nos objetos que queremos renderizar e muito provavelmente eles estão distantes da origem. Portanto, é nesse espaço que iremos garantir o que será exibido na tela. A tela, é composta pelos valores de largura e altura que sempre são positivas e que o seu "eixo" é no canto superior esquerdo da tela.
1.6- Espaço de Tela (Screen Space)
Espaço da Tela passaremos a trabalhar com coordenadas no Espaço Canônico.
No trabalho anterior, foi visto como passar coordenadas de tela. Ou seja, dar as coordenadas exatas dos pontos na tela do computador, mas não é assim que funciona na prática. O que acontece é que temos objetos modelados com coordenadas x e y, sejam negativas ou positivas, e queremos que isso seja mostrado na tela. Iremos entrar com as coordenadas dos nossos objetos no Espaço Canônico (variando no intervalo [-1,1]), e o nosso programa deverá conseguir transportar essas coordenadas no Espaço de Tela, a origem do eixo de coordenadas do Espaço Canônico deve ser o centro da tela, no Espaço da tela. a coordenada (0,0), no Espaço Canônico, deve ser a coordenada ((W-1/2), (H-1)/2) na tela, onde W representa a largura e H a altura da tela. E vale salientar Espaço de Tela “cresce” em X para a direita e em Y para baixo, e coordenadas do Espaço Canônico “crescem” em X para a direita e em Y para cima. Para realizar o conversão entre espaços é preciso ajustar o sistema de coordenadas da tela. Abaixo veremos uma ilustração:
No trabalho anterior, foi visto como passar coordenadas de tela. Ou seja, dar as coordenadas exatas dos pontos na tela do computador, mas não é assim que funciona na prática. O que acontece é que temos objetos modelados com coordenadas x e y, sejam negativas ou positivas, e queremos que isso seja mostrado na tela. Iremos entrar com as coordenadas dos nossos objetos no Espaço Canônico (variando no intervalo [-1,1]), e o nosso programa deverá conseguir transportar essas coordenadas no Espaço de Tela, a origem do eixo de coordenadas do Espaço Canônico deve ser o centro da tela, no Espaço da tela. a coordenada (0,0), no Espaço Canônico, deve ser a coordenada ((W-1/2), (H-1)/2) na tela, onde W representa a largura e H a altura da tela. E vale salientar Espaço de Tela “cresce” em X para a direita e em Y para baixo, e coordenadas do Espaço Canônico “crescem” em X para a direita e em Y para cima. Para realizar o conversão entre espaços é preciso ajustar o sistema de coordenadas da tela. Abaixo veremos uma ilustração:
Espaço Canônico Espaço da Tela
Figura 2 - Representação do Espaço Canônico e Espaço de Tela
2-Transformações Geométricas.
Como representar estas transformações geométricas?
Quando falamos de transformações geométricas, já vem a nossa mente os conceitos de translação, rotação e escala. Pois bem, é exatamente isto que iremos ver aqui, iremos montar equações lineares que transformarão os vértices e ainda tentaremos estender as equações para sua forma matricial.
2.2- Transformação de Escala
Figura 3 - Transformação de Escala
Pode ser entendida como a mudança de unidade de medida em uma ou mais dimensões, e para isso devermos multiplicaras de coordenadas por uma constante, que conhecido como fator escala, logo:
X' = X * Sx
Y' = Y * Sy
Z' = Z * Sz
Z' = Z * Sz
De forma matricial:
➦ Escalas:
➦ Escala isotrópica:
É quando o fator de escala são iguais(Sx=Sy), tem objetivo que objeto mude de tamanho proporcionalmente em todas as coordenadas.
➦ Escala anisotrópica:
É quando o fator de escala são diferentes(Sx!=Sy), tem objetivo de deformar ao mudar tamanho em todas as coordenadas.
➦ Espelhamento:
➦ Espelhamento em Y(Sx=1 e Sy=-1):
valor de escala deve ser 1 para Sx e -1 Sy.
➦ Espelhamento em x(Sx=-1 e Sy=-):
➦ Espelhamento em Y(Sx=1 e Sy=-1):
valor de escala deve ser 1 para Sx e -1 Sy.
➦ Espelhamento em x(Sx=-1 e Sy=-):
valor de escala deve ser -1 para Sx e 1 Sy.
Uma escala anisotrópica, tem objetivo de deformar ao mudar tamanho em todas as coordenadas.
2.1- Rotação

Figura 4 - Transformação de Escala
A rotação pode ser definida como um movimento de giro, num plano, em relação a um referencial. As rotações podem ser feitas nos três eixos de coordenadas, portanto seria necessário criar uma matriz para cada um dos tipos de rotação. Para ser mais didático iremos exemplificar no plano XY. A figura 5 mostra a rotação de um ponto P em torno da origem, passando para a posição P'.

Figura 5 -Ponto P rotacionado até o ponto P'
)
Que é equivalente as expressões:
De forma matricial:
vale salientar que para aplicar em um objeto, é necessário que o objeto esteja na origem dos eixos, caso contrário, essa operação fará com o objeto translade:

Figura 6 - Rotação, que resulta em uma translação

Figura 7 - Rotação com objeto que não se encontra na origem
No espaço tridimensional a rotação pode ser definida através da associação de um ponto com um vetor, que pode ser chamado de eixo.
Figura 8- Aplicara a rotação em qualquer plano(xy,yz,xz)

Figura 5 -Ponto P rotacionado até o ponto P'
Se um ponto P, distante 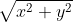 for rotacionado de um ângulo
for rotacionado de um ângulo 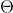 em torno da origem, antes da rotação as suas coordenadas eram definidas, assim:
em torno da origem, antes da rotação as suas coordenadas eram definidas, assim:
vale salientar que para aplicar em um objeto, é necessário que o objeto esteja na origem dos eixos, caso contrário, essa operação fará com o objeto translade:

Figura 6 - Rotação, que resulta em uma translação
Para rotacionar corretamente terá que fazer 3 passos
1)Transladar este ponto a origem dos eixos ➦ 2) Efetuar a rotação➦ 3) Transladar ao ponto para de sua posição de origem.
1)Transladar este ponto a origem dos eixos ➦ 2) Efetuar a rotação➦ 3) Transladar ao ponto para de sua posição de origem.

Figura 7 - Rotação com objeto que não se encontra na origem
Figura 8- Aplicara a rotação em qualquer plano(xy,yz,xz)
2.1- Transformação de Translação
A translação é um movimentar o objeto. para isso precisaremos adicionar quantidades as suas coordenadas. É possível efetuar a translação de pontos em (X,Y,Z) pode ser movido Tx unidades em relação ao X, e por Ty unidades em relação em Y e por Tz unidades em relação em Z, passando ser escrito em (X',Y',Z'), , logo, poderá ser escrito:
X' = X + Tx
Y' = Y + Ty
Z' = Z + TZ

Figura 10 - Translação de um triângulo de 3 unidades
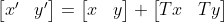
Z' = Z + TZ

Figura 10 - Translação de um triângulo de 3 unidades
a nova posição pode ser representado como:
Como pode ser visto na forma acima não encontra-se na forma matricial, abaixo explicarei a importância que essas transformações esterem na forma matricial.
O motivo que sempre estamos trabalhando na forma matricial, possibilita a composição de matrizes através do produto entre elas e que essa operações entra matrizes podem ser facilmente paralelizadas, e com isso pode usar a principal função de uma GPU(Graphics Processing Unit, ou Unidade de Processamento Gráfico). E Desta forma, é possível paralelizar as operações, acelerando o desenvolvimento do pipeline. Mas nos encontramos em uma situação aparentemente sem solução favorável, porquê assim não poderíamos fazer composições que envolvesse translação e seria extremamente custoso parar uma execução de operação (multiplicação matricial, por exemplo) para fazer uma operação completamente diferente como somar dois números . Logo teremos que fazemos uso das coordenas homogêneas
De forma matricial:
O motivo que sempre estamos trabalhando na forma matricial, possibilita a composição de matrizes através do produto entre elas e que essa operações entra matrizes podem ser facilmente paralelizadas, e com isso pode usar a principal função de uma GPU(Graphics Processing Unit, ou Unidade de Processamento Gráfico). E Desta forma, é possível paralelizar as operações, acelerando o desenvolvimento do pipeline. Mas nos encontramos em uma situação aparentemente sem solução favorável, porquê assim não poderíamos fazer composições que envolvesse translação e seria extremamente custoso parar uma execução de operação (multiplicação matricial, por exemplo) para fazer uma operação completamente diferente como somar dois números . Logo teremos que fazemos uso das coordenas homogêneas
Coordenadas homogêneas
Com objetivo de permitir que quaisquer das três transformações sejam realizadas com multiplicações e, com isto, tornar possível a combinação de todas elas numa única matriz foi criado o conceito de coordenadas homogêneas.
Com objetivo de permitir que quaisquer das três transformações sejam realizadas com multiplicações e, com isto, tornar possível a combinação de todas elas numa única matriz foi criado o conceito de coordenadas homogêneas.
Para conseguir escrever uma transformação de Translação de forma matricial são usadas as Coordenadas Homogêneas, isso significa o tamanho do vetor terá um acréscimo de uma dimensão, ou seja, vetores serão representados por n+1 coordenadas, onda a sua última coordenada será denominada de Homogênea(W), por exemplo: (X,Y,Z) passará (X,Y,Z,W). Caso queria, transformar de Coordenadas Homogêneas para o Espaço Euclideano, basta dividir as coordenadas XY pela homogênea. Exemplo: (x,y,,z,w) ➦ (x/w, y/w, z/w)
De forma matricial:
Sendo assim, serão reescritas as matrizes de Escala, Rotação e de Translação
Espaço Euclideano Espaço Homogênio w=1 Espaço Honogênio
(x,y,z) ➦ (xw,yw,zw,w) ➦ (x, y, 1)
Abaixo, pode ser vista todas as transformações em forma matricial no espaço de 3 dimensões, fazendo uso da variável W do espaço homogêneo.
Escala:
Escala:
Rotação em X:
Rotação em Y:
Rotação em Z:
Foram desenvolvidas classes manipulação de vetores e matrizes, alguns operadores foram sobrecarregados, como por exemplo multiplicação(*) e adição (+).
Matrizes de Transição:
Como já foi explicado no Espaço do Universo, consiste trazer os vértices dos objetos que vai formar a cena do modelo cartesiano em 3D. Essa transformação é aonde acontece as alterações no nosso vértice geral que funcionam como edições. Para sermos capaz de realizar essas transformações temos que multiplicar nossos vértices originais por determinadas matrizes de transformação, foi utilizada a matriz model, como pode ser visto abaixo:
Quando nossos vértices estão no Espaço do Universo, temos nossa cena para representada-la, e para isso será preciso especificarmos a configuração câmera.
Agora, vamos focar nas operações realizadas para encontrar os Eixos do Espaço da Câmera e posteriormente as transformações que ocorrem no mesmo. E para isso utilizaremos a matriz View. Esta matriz é responsável pela posição da câmera e para onde ela aponta, e o centro da cena passa a ser a posição da câmera, antes definir a nossa Matriz View, devemos configurar a câmera, para isto devemos ter armazenadas certas informações sobre a câmera:
Posição da Câmera (Camera Position): Está é a posição da câmera ainda no espaço do Universo, pois lembre-se que ela sempre está na origem no espaço da Câmera. Este posicionamento, será composto por valores dos eixos coordenados x, y e z. Como mostrado abaixo:
camera_Posicao=(Px,Py,Pz)
Direção da Visão (View Direction): Agora iremos informar aonde a câmera está mirando, ou seja, para qual lugar a visão dela está direcionada. Assim, como na posição da Câmera, ainda estamos considerando que a câmera está no espaço do Universo. Desta forma, caso o objeto a ser visualizado esteja na origem, a direção de visualização da câmera será (0, 0, 0).
VetorUP : O vetor UP é ele informa qual é a "parte de cima" da cena. Como na maioria das vezes o Up é o eixo Y, geralmente este vetor sempre terá valor (0, 1, 0).
camera_LookAt=(Dx,Dy,Dz)
VetorUP : O vetor UP é ele informa qual é a "parte de cima" da cena. Como na maioria das vezes o Up é o eixo Y, geralmente este vetor sempre terá valor (0, 1, 0).
camera_Up=(Ux,Uy,Uz)
Depois que configuramos a câmera, agora usaremos a matriz mView é composta por mais duas matrizes auxiliares, uma de rotação e outra de transalação, multiplicadas uma pela outra e que transferem o centro da cena para a posição da câmera, previamente definida (discutiremos mais a frente).
2.3- Espaço da Câmera ➦ Espaço Projetivo ou de Recorte:
Tendo os vértices já no Espaço da Câmera, utiliza-se mais uma matriz chamada de Matriz de Projeção (Projection), que irá trazer os pontos para o Espaço de Corte.Como sabemos, nossa câmera aponta para um ponto específico da cena. Sendo assim, teremos duas opções de visualização, uma com distorção perspectiva e outra sem.Vale salientar, que a câmera também tem um certo ângulo de visão, chamado aqui de “abertura da câmera", que significa sempre que posicionamos uma câmera, ela registrará um volume da cena.Basicamente o queremos agora transformar seu sistema de coordenadas para o espaço projetivo, e para isso utilizamos a matriz Projeção. Esta matriz faz com que os vértices do espaço da câmera sejam projetados em um plano de projeção, o View Plane. Aqui a coordenada homogênea é alterada.
2.4- Espaço Projetivo ➦ Espaço Canônico:
Logo depois de aplicarmos a projeção perspectiva é necessário realizar a homogeneização dos vértices, ou seja, dividir todos pela coordenada homogênea W, isto significa uma mudança na geometria da cena fazendo com que toda a cena uma distorção perspectiva, os objetos próximos da câmera ficam maiores, e os mais afastados ficam menores.
2.5- Espaço Canônico ➦Espaço de Tela:
Por fim, aqui queremos transformar os vértices do espaço canônico para o espaço da tela, isto é feito através da multiplicação dos vértices por uma matriz que contém duas escalas e uma translação. A imagem abaixo ilustra as diferenças entre os vértices no espaço canônico e no espaço de tela tornando mais fácil a compreensão dos passos necessários para levar os vértices de um espaço para o outro. A imagem abaixo ilustra bem as diferenças entre os vértices no espaço canônico e no espaço de tela.

Resultado:

Dificuldades encontradas no Trabalho
A maior dificuldade enfrentada nesse trabalho foi em relação a interpolar as cores.
Possíveis melhoras
"Limpar o código", tendo em vista que código é didático, foi criado variáveis sem utilidade efetiva.
Referências
PAGOT, Christian Azambuja. Material de aula . 30 mar. 2015, 11 may. 2015. Notas de Aula.
Tags: Pipeline Gráfico, Computação Gráfica, Graphic Computer ,CG, Programação, programming, colorbuffer, framebuffer, Opengl, Pipeline Gráfico, C++, T2 , segundo trabalho de computação gráfica UFPB, Pipeline Gráfico em C++












Comentários
Postar um comentário
comenta aqui